今回の問題は、標準編ですが入試レベルの問題です。頑張って行きましょう!
例題1
長さ20mの木を2mずつに切り分けます。1回切るのに6分かかり、1回切るごとに2分間の休憩を取るとき、何分で切り終えることができますか?
まず、簡単な数字で置き換えて考えてみましょう。
長さ3mの木を1mずつ切り分けると考えます。
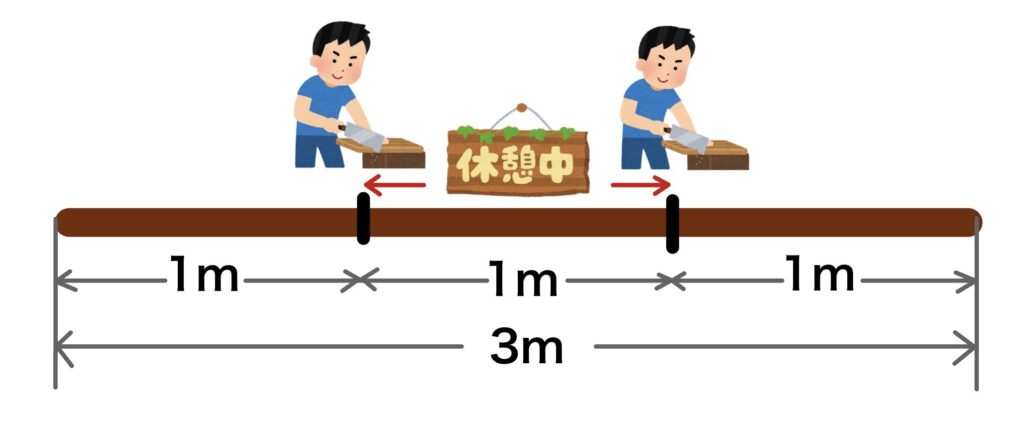
①間の数〔木材の数〕=3(3÷1)
②区切りの数〔切る回数〕=2
③区切りの間の数〔休憩の回数〕=1
①②③はそれぞれ前の数字から−1をした数になる事が分かりました。
本題に戻りましょう。
①間の数〔木材の数〕=10(20÷2)
②区切りの数〔切る回数〕=9(間の数−1)
③区切りの間の数〔休憩の回数〕=8(区切りの数−1)
したがって、20mの木を切り分けるには
6×9+2×8=70
20mの木を切り分けるには70分かかります
例題2
ある道のはしからはしまで一定の間隔で木を植えます。20mの間隔で木を植えると、30mの間隔で木を植える時よりも20本多くの木が必要になります。この道の長さは何メートルですか。
〔道路の長さ〕÷〔木の間隔〕+1(←区切りの数を求めるため)=区切りの数
❶□÷20+1=20m間隔で植えた時の木の本数
❷□÷30+1=30m間隔で植えた時の木の本数
❶は❷よりも20本、木の本数が多いので式は以下のようになります。
□÷20+1=□÷30+1+20
□を出すための計算方法はぜひ動画を確認してみて下さい。
□=1200
道の長さは1200mです。
例題2(別解)
別解では最小公倍数を用います。
まず、道路の長さを20と30の最小公倍数で仮定します。
公倍数を順に並べて、それぞれの木の本数の差を出します。
道路の長さと木の本数の差から関係性を導きます。
下の表を見てみましょう。
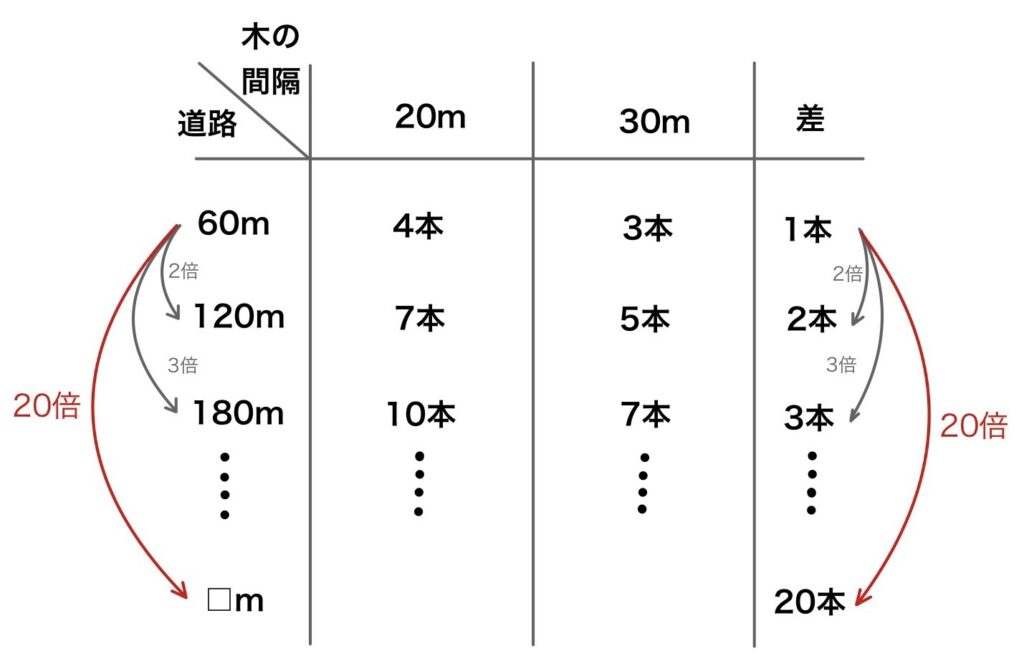
道路の長さが2.3倍になると、差も2.3倍になることが分かります。
したがって、差が20本になるのは最小公倍数を20倍した数なので
答えは1200mということが分かります。
例題2では、虫食い算を使って答えを求める方法と最小公倍数を用いて答えを求める方法を学習しました。
自分に合った考え方で答えを導けるようにしっかりと復習しましょう!
