例題1
ある池のまわりをA君とB君が反対方向に向かって同時に出発します。A君が分速50m、Bくんが分速30mで歩いたところ、10分後に出会いました。池のまわりは何mですか?
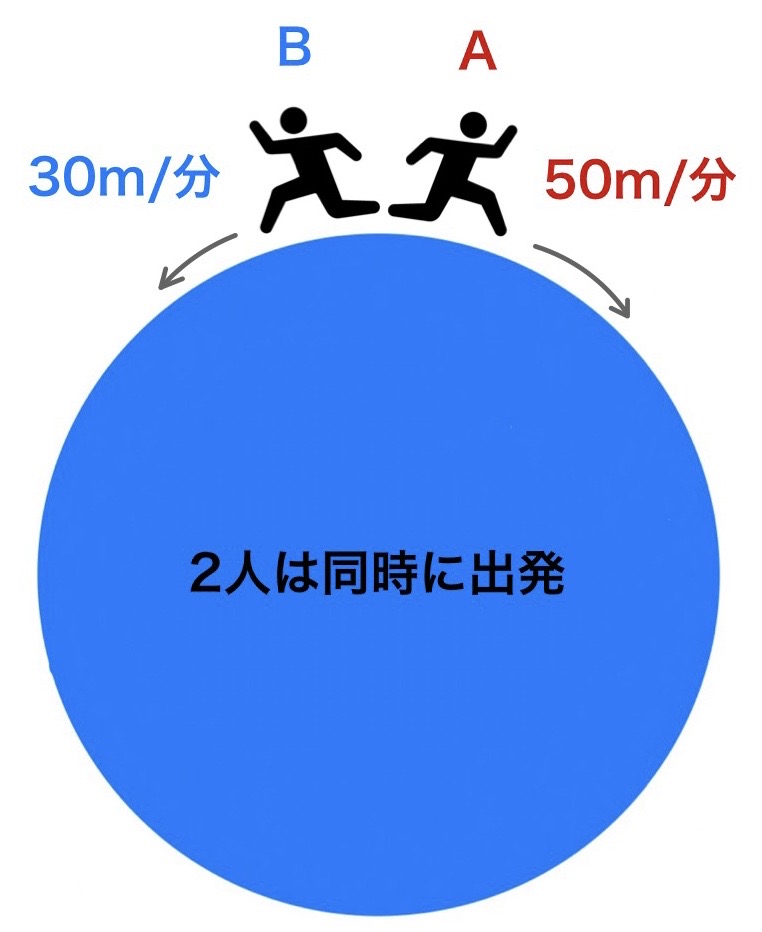
池のような円周上の動きは旅人算によく出るパターンです。
この問題では“2人がどのくらい離れていったか”に着目しましょう。
AB間の距離は出発して1分後80m、2分後160m、3分後240mです。
つまり、(Aの速さ)+(Bの速さ)分だけ離れていきます。
したがって10分後は
( 50m/分 + 30m/分 )× 10分後 = 800m
池のまわりは800mです。
例題2
太郎と次郎の家は道に沿って1.9km離れています。次郎が8:00に家を出て太郎の家に向かいました。太郎は8:04に家を出て次郎の家に向かいました。二人は何時何分に出会いますか?ただし、太郎の分速は65mで次郎の分速は70mです。
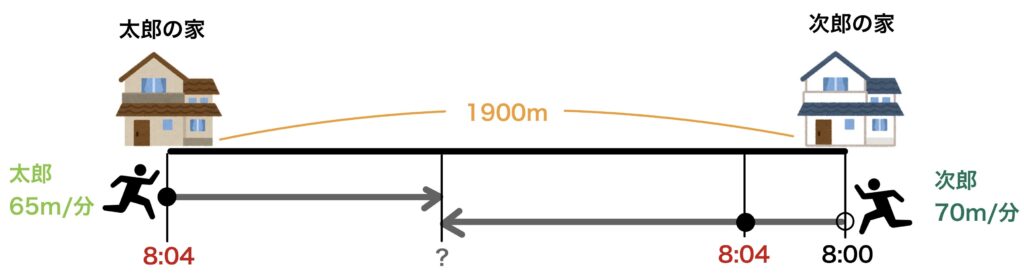
旅人算の考え方を用いるのは2人以上の人やモノが動いている時です。
1人だけが動いている時は速さの基本的な求め方で求めることができます。
したがって、この問題では8:00から8:04は速さの問題として考えます。
まず、簡単な図を書いてみましょう。
この時、時間ごとに記号を変化させることと、単位を統一する事がポイントです。
次郎が8:00から8:04までに進んだ距離は次のように求める事ができます。
70m/分 × 4分 = 280m
8:04分の時点で次郎と太郎の間の距離は
1900m−280m=1620m
です。
2人が進んだ距離の和が1620mになるのは何分後かを求めます。
(65m/分+70m/分)× □分 = 1620m
□=12
8:04の地点から2人が出会うまでに12分かかったことが分かりました。
したがって、8:04の12分後に2人が出会ったのは8:16です。
