舟で川を漕ぐとき、上りと下りで速さが異なることが想像できますよね?
なぜでしょう?
速さが異なるのは、舟を漕ぐスピードに加えて川の流れる速度が影響するためです。
「流水算」はこれらを考慮して解く問題の際に用いられます。
流水算は他に、動く歩道やエスカレーターの上り下りなどでよく出題されます。

流水算では4つの速さを整理することが重要になります。
・静水時の速さ(流れがない場所で舟を漕いだ時の速さ)
・上りの速さ(下流から上流に向かう速さ)
・下りの速さ(上流から下流に向かう速さ)
・流速(川の流れる速さ)
下りの速さと上りの速さは以下の式で求めることができます。
下りの速さ=静水時の速さ+流速
上りの速さ=静水時の速さ−流速
流水算では線分図を用いて4つの速さを整理しましょう。

例題1
ある船が30kmある川を6時間で下りました。同じ川を上るのに10時間かかりました。次の問いに答えなさい。
① 下りの速さは時速何kmですか?
②上りの速さは何kmですか?
③川の速さは時速何kmですか?
④静水時の船の速さは時速何kmですか?
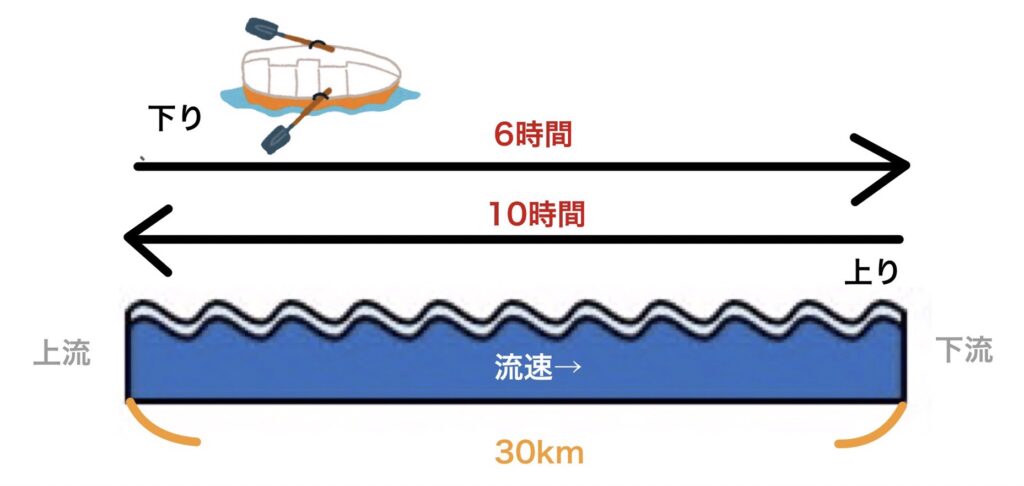
①30kmの川を6時間で下るので、速さの公式を用いると
30km ÷ 6時間 = 5km/時
下りの速さは時速5kmです。
② ①同様に速さの公式を用いると
30km ÷ 10時間 = 3km/時
上りの速さは時速3kmです。
③川の速さ=流速です。
①②より、線分図は以下のようになります。

下りの速さは、上りの速さに流速を2つ分足したものであることが分かります。
したがって、
〔下りの速さ〕−〔上りの速さ〕= 流速×2
5km/時 − 3km/時=2km/時
流速は
2km/時 ÷ 2=1km/時
川の速さは時速1kmです。
④静水時の船の速さは線分図を見ると分かるように
上りの速さ+流速 あるいは 下りの速さ−流速
つまり、
3km/時 + 1km/時=4km/時
5km/時 − 1km/時 = 4km/時
静水時の船の速さは時速4kmです。
例題2
静水を漕ぐ速さが時速10kmの人が3時間で45km漕ぎ下りました。次の問いに答えなさい。
①流れの速さは時速何kmですか?
②上りの速さは時速何kmですか?
③この川を3時間漕いで上ると何km進みますか?
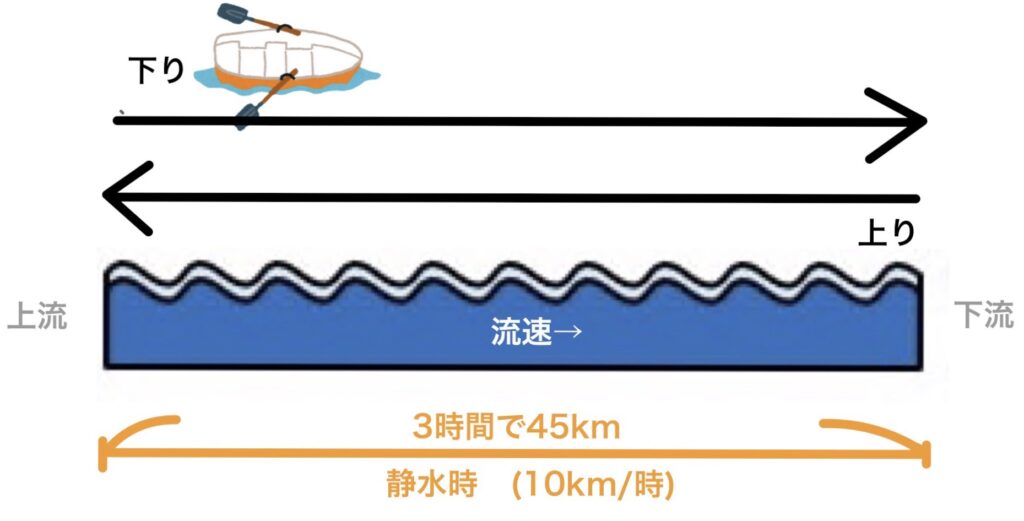
①まず、距離と時間が出ているので下りの速さが求めることができます。
速さの公式より、
45km/時 ÷ 3時間 = 15km/時
ここで線分図を書いて見ましょう。

上図から流れの速さ(=流水)が求められます。
15km/時 − 10km/時 = 5km/時
流れの速さは時速5kmです。
②線分図から、
上りの速さ=〔静水時の速さ〕−〔流速〕で求めます。
10km/時 − 5km/時 = 5km/時
上りの速さは時速5km/時です。
③ ②で上りの速さが出ているので、速さの公式を用いて距離を求めます。
5km/時 × 3時間 = 15km
この川を3時間漕いで上ると15km進みます。
流水算は3本の線分図を用いて4つの速さを整理することがポイントです。
上りと下りはそれぞれ“流速の影響を受ける”ことを意識しましょう。
