標準編の時計算では、
時計の長い針と短い針がぴったり重なるのはいつか?
時計の長い針と短い針が作る角度が◯◯度の時、何時何分か?
について考えます。
混乱した時には池の周りを長い針と短い針が追いかけっこするイメージで考えてみると良いでしょう。

例題1
(1)4時に時計の長い針と短い針の作る角で小さい方の角の大きさは( )度です。
(2)4時と5時の間で時計の長い針と短い針が重なるのは、4時( )分です。
(2)のように◯時から◯時の間で長い針と短い針が重なる時間を考える時にはピッタリした時間を考える。(1)は(2)を解くためのヒントになる。
(1)時計の数字1つ分は30°なので4時の時点で作られる角度は次の式で求められる。
30° × 4つ分 = 120°
角度は120°です。
(2)まず、考えられる状況を簡単に書いてみましょう。(左図)
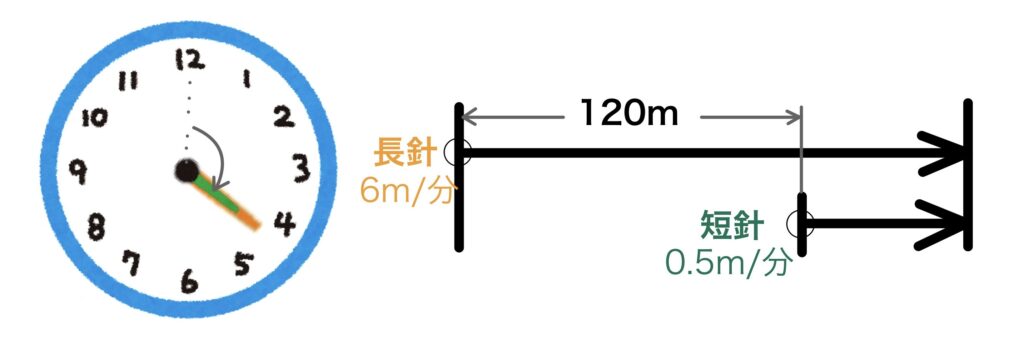
時計の度数を距離と考えると右図のように整理する事ができます。
2つの針が進んだ後、120m差になる時間がつまりこの問題の解答になることが分かりました。
この考え方は旅人算と同じです!
したがって、
120m ÷( 6m/分−0.5m/分 )= 120/5.5 = 240/11 = 21 9/11
答えは4時21 9/11分です。
例題2
(1)9時と10時の間で時計の長い針と短い針の重なる時刻は9時( )分です。
(2)9時と10時の間で12時の目盛りを挟んで左右対称の位置のなる時刻は9時( )分です。
(1)は例題1(2)と同様に考える。
ピッタリ9時の時、長い針と短い針が作り出す角は270°である。(大きい方の角)
短い針は長い針の270°分だけ先にいると考えればいいので
270° ÷( 6m/分−0.5m/分 )=270/5.5=540/11=49 1/11
したがって時刻は9時49 1/11分です。
(2)求める時刻は線対称、つまり12時の軸を対称軸として反転すると長い針と短い針が重なり合う。
長い針が動いた角度をa、短い針が動いた角度をbとする。
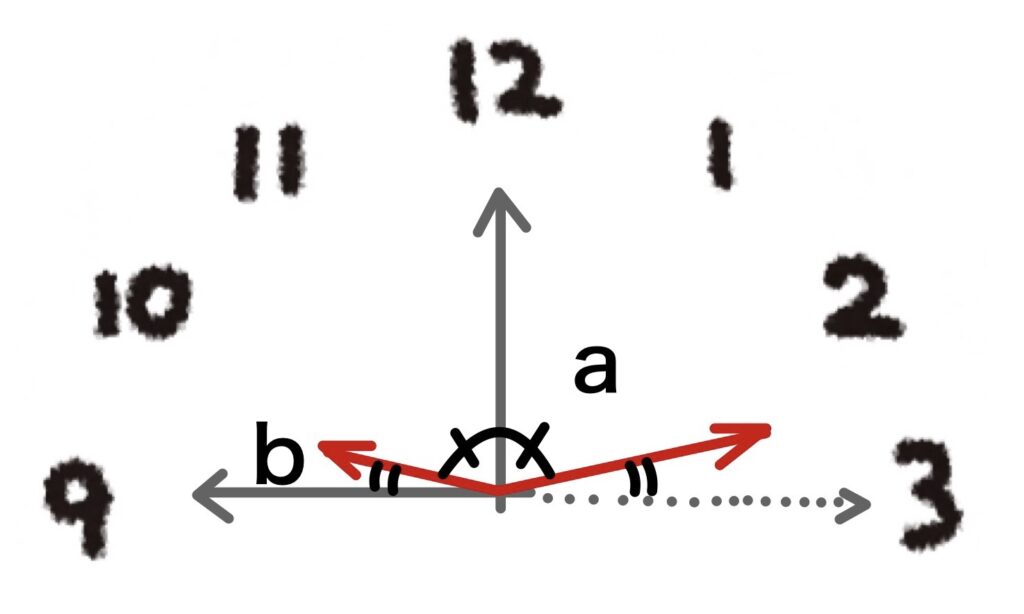
今回の問いでは長い針と短い針が動いた角度の和を考える。
上図より、
a=直角からbを引いた角度
b=直角からaを引いた角度であり、
a + b = 90°
したがって、“短い針と長い針の進んだ角度の和が90°になるのは9時( )分”かと問題を読み変える事ができる。
90° ÷( 6°/分 + 0.5°/分 )=90/6.5=180/3=13 11/13
したがって時刻は9時13 11/13分です。
時計算の標準編では進んだ距離の和が問題になっているのか、差が問題になっているのかに着目して復習してみましょう。
