時計算について、こちらの動画の内容に沿って解説を致します。
「時計算」は、長い針と短い針がどのように動くかを考え、2つの針が作り出す角度を使った問題です。
時計算では、“ある時間から針が作る角度”を求めたり、“ある角度から時間”を求めたりできるようになりましょう。
時計の針は絶えず動いていることを忘れないようにしましょう。

例題1
(1)時計の長い針は1時間に( )度動き、1分間に( )度動きます。
(2)時計の短い針は1時間に( )度動き、1分間に( )度動きます。
(1)時計を想像して見てください。
針が1周すると360°ですよね?
長い針は1時間で360°動きます。
1時間=60分なので、1分間あたりに動く角度は以下の式で求めます。
360° × 1/60分 = 6°
時計の長い針は1時間に(360)度動き、1分間に(6)度動きます。
(2)短い針は1時間で数字1つ分動きますよね?
数字1つ分は何度でしょうか?
数字は1から12まであります。したがって、1つ分の角度を求めることができます。
360° ÷12 = 30°
1分間に動く角度は(1)で求めた時と同じ考え方を用いて、
30° × 160分 = 12°(0.5°)
時計の短い針は1時間に(30)度動き、1分間に(0.5)度動きます。
例題2
(1)8時に時計の長い針と短い針の作る角で、小さい方の角の大きさは( )度です。
(2)10時10分に時計の長い針と短い針の作る角で、小さい方の角の大きさは( )度です。
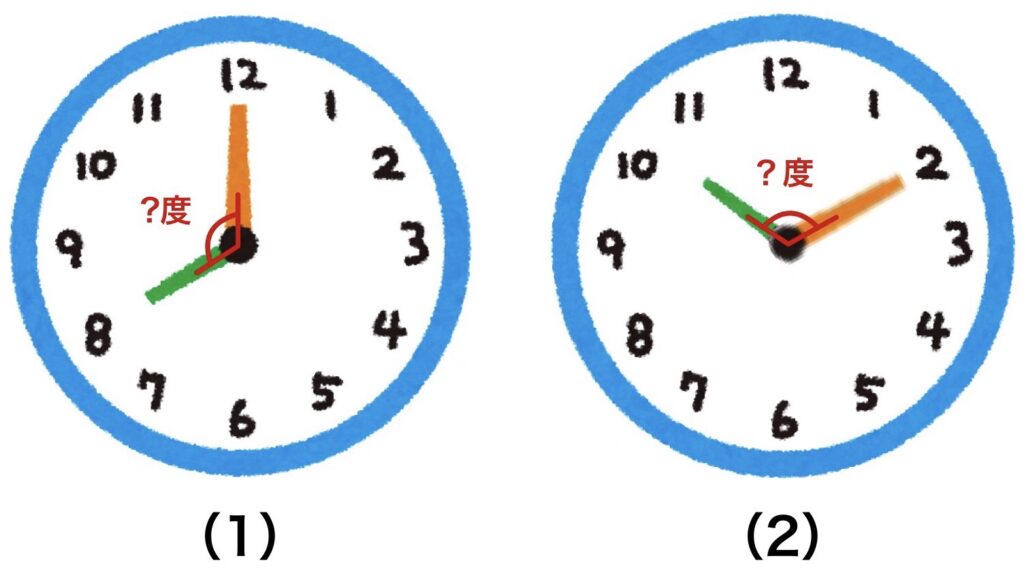
(1)まずは簡単に8時の時点での針を書いて見ましょう。
全ての数字を書く必要はありません!!
数字と数字の間隔は30°であると分かっていますよね?(例題1より)
8時の時、長い針と短い針の間隔は4つ分なので
30° × 4= 120°
求める角の大きさは120°です。
(2)この問題でも、簡単に10時10分時点での針を書いて見ましょう。
この時、短い針を10と11の数字の間に書くことがポイントです。
長い針は10時10分の時、ピッタリ2にいますよね。
短い針はピッタリの時間からどのくらいの角度ずれたかを考えましょう。
1分あたり0.5°動くことが分かっているので(例題1より)10分間では
05° × 10分 = 5°
10分間で5°動くことが分かりました。
長い針と短い針の間隔は、5°だけ小さい4つ分なので式は以下のようになります。
30° × 4 − 5° = 115°
求める角の大きさは115°です。
時計算では実際の時計を思い浮かべ、柔軟に対処できるようにしましょう。
