旅人算について、こちらの動画の内容に沿って解説を致します。
「旅人算」とは、ふたり以上の人が一直線上で同じ方向に動いたり、向かい合って(あるいは背中を向けて)動いたりする場合に用いられる考え方です。
旅人算でポイントになるのは、ふたりの間の距離がどうなるかと言うことです。
Aさんが分速20m、Bさんが分速30mで進むとします。
①同じ方向に進むとき(A.Bさんが同じ地点からスタート)
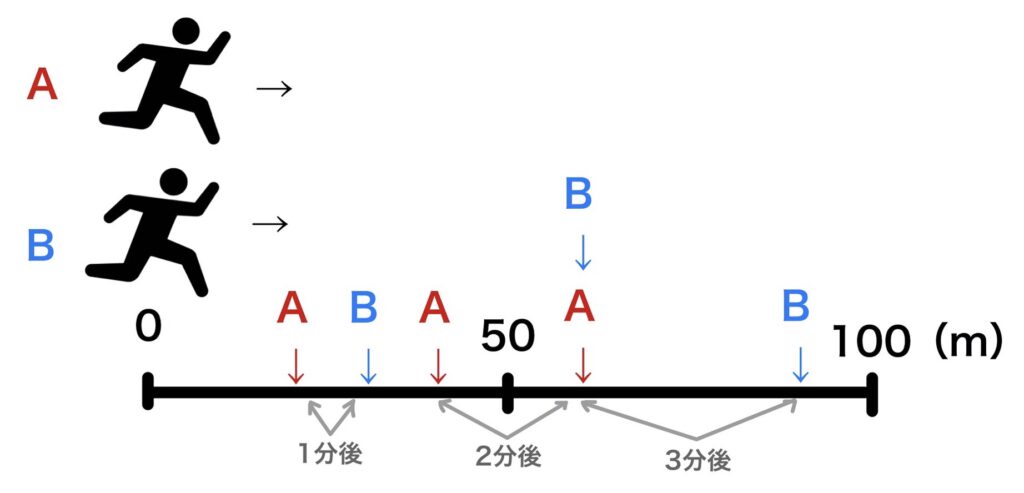
AB間の距離は1分後10m、2分後20m、3分後30m、、
②異なる方向に進むとき(Bさんは250m離れたところからスタート)
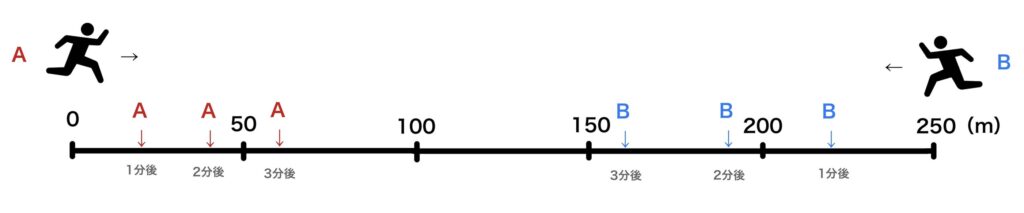
AB間の距離は1分後200m、2分後150m、3分後100m、、
上の2つの図から1分あたりに変化する距離を推測することができます。
①AB間は1分間で10mずつ変化⇨ABの速さの差
②AB間は1分間で50mずつ変化⇨ABの速さの和
したがって、1分間あたりに変化する距離は速さの差/和で表すことができます。
似たような問題に速さの問題があります。
速さの問題と旅人算の違いは、動く対象が1人か2人かと言う違いです。
旅人算の問題を解く際には、簡単な図を書くことをオススメします。
その際、
1.速さ(秒速/分速/時速)
2.進む方向
3.スタートしたタイミング
の3つの情報は必ず書き込みましょう。
例題1(1.向かい合って進む場合)
A君とB君は400m離れた地点から向かい合って同時に出発します。A君が分速50m、B君が分速30mの時、二人が出会うのは出発してから何分後ですか?

AB間の距離は二人の速さの和だけ変化します。
1分間あたりに変化する距離=速さ
なので立式すると
(50m/分 + 30m/分)× □分 = 400m
□=5
二人が出会うのは5分後です。
例題1(2.異なる方向に進む場合)
A君とB君は同じ地点から反対方向に向かって同時に出発します。A君が分速50m、B君が分速30mのとき二人の距離が400mになるのは出発してから何分後ですか?

AB間の距離は二人の速さの和だけ変化します。
したがって、
(50m/分 + 30m/分)× □分 = 400m
□=5
5分後に二人の距離が400mになる。
お気づきでしょうか?
これは例題1の1と同じ式で求めています。
つまり、近づいてくる問題も遠ざかっていく問題も考え方は同じです。
例題2(1.同じ方向に違うスタート地点から進む場合)
A君は100m前にいるB君を追いかけます。A君が分速50m、B君が分速30mのとき、A君が出発してから何分後にB君に追いつきますか?

1分間後二人の距離は80mで、スタート時と比較して20m分距離が縮まったことになります。
つまり、AB間の距離は二人の速さの差だけ変化します。
(50m/分 − 30m/分)× □分 =100m
□=5
A君がB君に追いつくことのは5分後になります。
例題2(2.同じ方向に同じスタート地点から進む場合)
A君とB君は同じ地点から同じ方向に向かって出発します。A君が分速50m、B君が分速30mの時、二人の距離が200mになるのは出発してから何分後ですか?

AB間の距離は二人の速さの差だけ変化します。
したがって
(50m/分 − 30m/分)× □分 = 200m
□=10
出発してから10分後に二人の距離は200mになります。
旅人算は速さの差/和を考慮して、速さの公式「速さ×時間=距離」に当てはめることで対応できます。
問題の状況をしっかり理解して正解を導き出しましょう。
